Position, distance and displacement
What is distance?
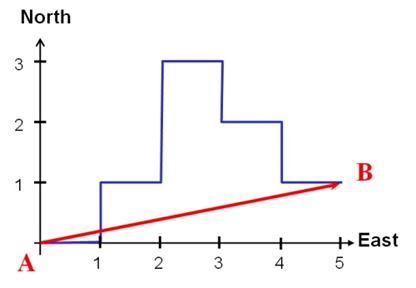
Distance is a scalar measure of the interval between two locations measured along the actual path connecting them.
Scalar measurements are measurements that simply have a magnitude (size).
What is displacement?
Displacement is a vector measure of the interval between two locations measured along the shortest path connecting them.
Vector measurements, like displacement, are measurements that have both magnitude (size) and direction.

How to calculate displacement?
Displacement, s, is defined as the change in position, r, of an object in a given direction. We calculate change in quantities by subtracting the initial quantity from the final quantity:
s = rfinal– rinitial
Usually, we can define the initial position of the object as zero, or “the origin” of the object.
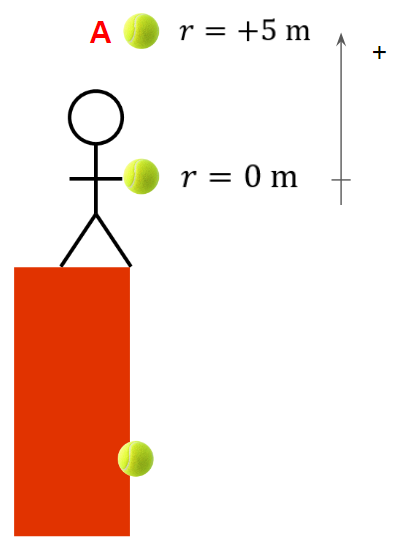
In this example, the ball’s initial position is in the student’s hand, where it has a displacement of zero.
When the ball is at position A, the displacement is:
s = 5 – 0 = 5 m
What is negative position?
Because displacement is a vector, we need to account for direction. We use the sign of the number to indicate direction.
The direction of displacement is either positive or negative for straight line motion. We assign positive values to any direction we want, usually in a way that makes our calculations simple.
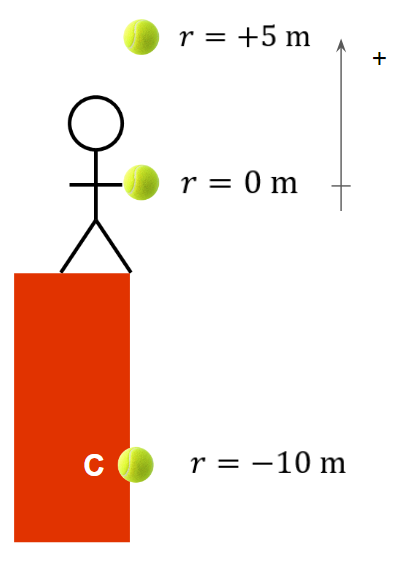
In this example, we have set the origin as the height of the student’s hand and assigned positive values to positions which are upwards.
Thus, then the ball is in position C, it’s position r = -10 m.
What is negative displacement?
Negative displacement values simply indicate displacements in the opposite direction. In this case, downwards.
Always include the negative sign in your calculations.

The student tosses the ball vertically upwards. What is the displacement of the ball when it is in position C?
The ball falls from position A to position C. What is the displacement of the ball?
Does the position of the origin matter? (advanced)
We usually define the initial position of the object as zero, or “the origin” of the object but we can define the origin wherever is convenient.
In this example, the ground beneath the cliff is used as the origin so the ball’s initial position (in the student’s hand),
r = +10 m.
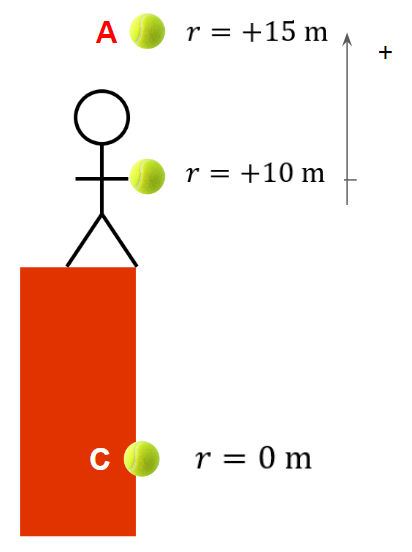
The student tosses the ball vertically upwards. What is the displacement of the ball when it is in position C?
The ball falls from position A to position C. What is the displacement of the ball?
Speed
What is the formula for average speed?
The formula for average speed is:
In symbols:
What are SI units?
The units in Physics are very important. Some formulae only work with certain units and you will get the wrong answer if you do not use the correct units!
Physics uses the International System of Units (SI = Système International in French), which is the modern metric system. The SI units are mostly easy for us because we live in Australia!
| Measurement | Units (abbreviation) |
| Distance | metres (m) |
| Time | seconds (s) |
| Mass | kilograms (kg) |
| Temperature | Kelvin (K) (but we can often use °C) |
What are the units of speed?
The SI units for speed are metres per second, abbreviated as m/s.
You will also see the units written as m s-1 (e.g. on your external exam information sheet). This is because we use negative indices in maths to indicate division, so:
Note that we don’t write multiplication symbols in units, and the units are separated by a space.
How to convert units?
When solving problems about speed we often need to convert from km/hr to m/s.
To convert from km/hr to m/s you simply multiply by 1000 and divide by 3600. (Note that this is the same as dividing by 3.6). It will help you to remember if you know how this works: because there are 1000 metres in a km and 3600 seconds in an hour.
Here is the maths behind the conversion (advanced):
How to convert from m/s to km/hr? Multiply by 3.6
What is instantaneous speed?
Speed (instantaneous) is the rate of change of distance with time.
We can express this idea using calculus, which you don’t need to know for this course!
The instantaneous speed of an object can be measured using technology like a radar gun.
Note that the instantaneous speed of an object can be determined without calculus by analysing its motion on a graph.
How can we calculate instantaneous speed from a graph?
In graphs of the distance of an object over time, the gradient of the line shows the rate of change of distance, which is the speed!
Remember, to find a speed, we need to measure both the distance and the time intervals. This means that every measurement of speed is really a measurement of some average speed.
However, if the time interval is very small, the average speed becomes very close to the instantaneous speed: vinst ≅ vavg

If the time interval is made smaller and smaller to that it approaches zero, the value of the vavg being measured approaches the gradient of the distance vs time graph.
Velocity
What is the difference between speed and velocity?
Velocity is the vector equivalent to speed. Thus, velocity has both magnitude and direction.
Speed tells you how fast. Velocity tells you how fast and in what direction.
We use displacement rather than distance to calculate velocity:
The units of velocity are the same as the units for speed.
We’ll use the symbol v for both speed and velocity because they’re related. To distinguish between velocity and speed, we can use an arrow above the symbol for velocity and displacement:
In the Physical Sciences course though, we use the same formula as the formula for speed:
What are scalar quantities? – Review
Scalar quantities are those that only have a magnitude
E.g.
- A distance measurement is given in metres – Sam walked 2 km to school.
- A mass measurement is given in kilograms – The car has a mass of 1500 kg.
Think, pair share: more example of scalar quantities…
How do we know the direction of velocity?
Because velocity is a vector, we need to account for direction. For straight line motion, an object is either travelling in one direction or the opposite direction. When we calculate velocity, it will be either positive or negative, which tells us the direction of velocity.
We assign positive values to any direction we want, usually in a way that makes our calculations simple.
In this example, a ball is thrown vertically upwards (the drawing shows the ball slightly offset for clarity)
Positive values indicate velocities upwards. The initial velocity is +5 m s-1.

Displacement-time graphs
Why use displacement-time graphs?
Using motion graphs, we can estimate the displacement, velocity and acceleration of a moving object at any instant without using calculus.
Displacement-time graphs plot the displacement of an object against time.
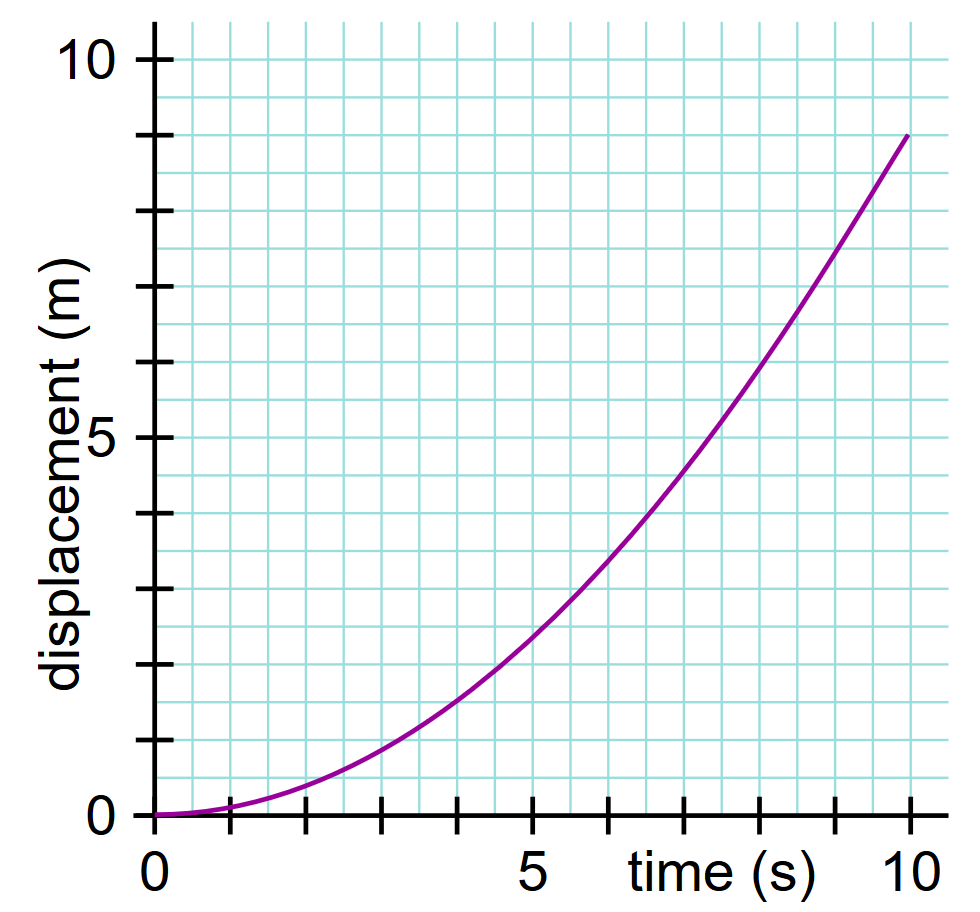
The slope of a displacement-time graph is equal to the velocity!
How to calculate instantaneous velocity from a tangent?
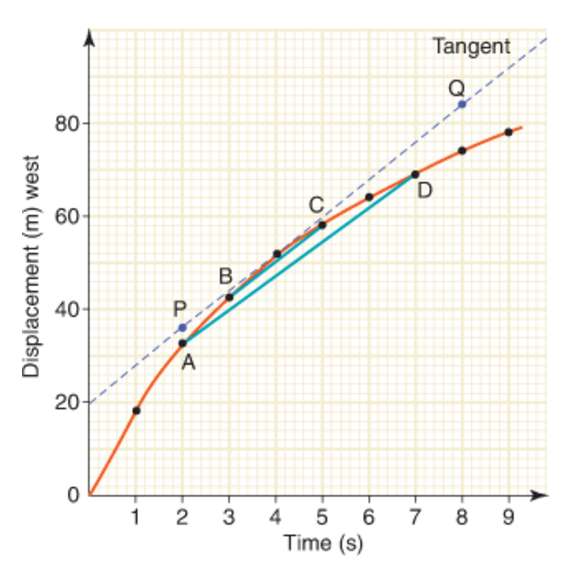
Acceleration along a straight line
What is acceleration?
Acceleration is the rate of change of velocity (e.g. how much the velocity changes every second).
Since velocity is a vector, acceleration is a vector.
- ∆v = change in velocity (m s-1)
- t = total time (s)
- u = initial velocity (m s-1)
- v = final velocity (m s-1)
What is negative acceleration?
Negative acceleration occurs when the velocity values are changing in the opposite direction to positive velocities. The direction of the acceleration makes much more sense when we study forces because objects always accelerate in the direction of the net force. When acceleration is negative:
- positive velocities decrease (e.g. after the ball leaves the physicist’s hand and is moving upwards).
- Positive velocities continue to decrease towards zero (e.g. as the ball reaches its maximum height and stops), then become negative (e.g. as the ball starts to fall downwards)
- negative velocities become increasingly negative (as the ball falls faster and faster).
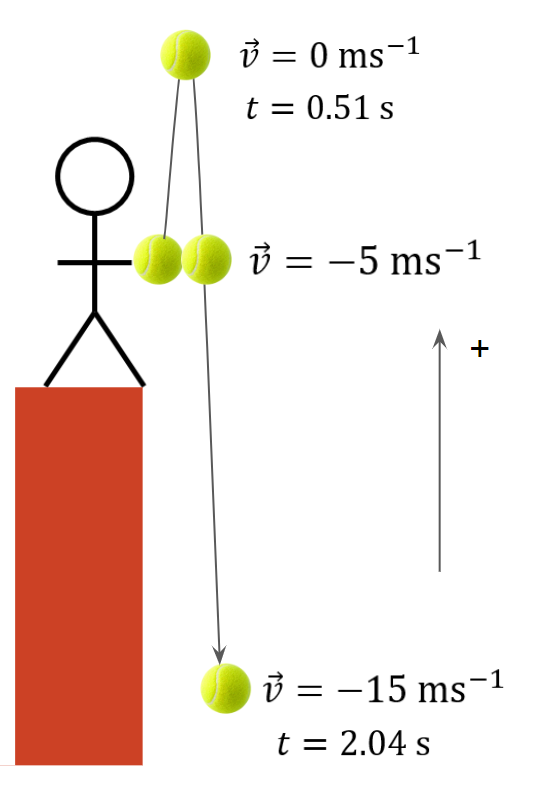
Negative accelerations result because acceleration is a vector.
For example, a ball is thrown upwards with initial velocity
u = 5 ms-1. Its velocity decreases and it reaches its maximum height (v = 0 ms-1) 0.51 s later. It’s acceleration is:
Two seconds after tossing the ball, the velocity is -15 ms-1 and its acceleration is:
Constant acceleration equations
What are the constant acceleration formulae?
These are also known as the suvat equations.
The quantities in these equations are vectors (except for time) but as long as the motion is in a straight line, vector notation is not necessary.
We can use positive or negative signs to indicate direction. Just choose a sign convention (which direction to call positive) and then remain consistent throughout the calculation.
Gravitational acceleration
What is gravitational acceleration?
The acceleration due to gravity, g = 9.81 m s-2 downwards on Earth (assuming zero air resistance)
We’ll find out why this is the case later in the course.
How can we describe the motion of falling objects?
Consider an object which has been dropped close to the surface of the Earth and is falling.
The object is moving in one dimension only (in a straight line up/down) and it is experiencing uniform (constant) acceleration.
- In the absence of air resistance, the value of the acceleration is 9.81 m s-1.?
We can use the equations of motion (for constant acceleration) to analyse motion in one dimension
Velocity-time graphs
Velocity – time graphs
Velocity-time graphs and speed-time graphs look identical, but velocity time graphs will give a direction on the vertical axis, and can have negative values.
They plot the velocity of an object at each instant of time
(Don’t look at these graphs and think of them as a picture of a moving object. Instead, think of them as the record of an object’s velocity. In these graphs, higher means faster not farther. The v = 9.0 m/s line is higher because that object is moving faster than the others.)
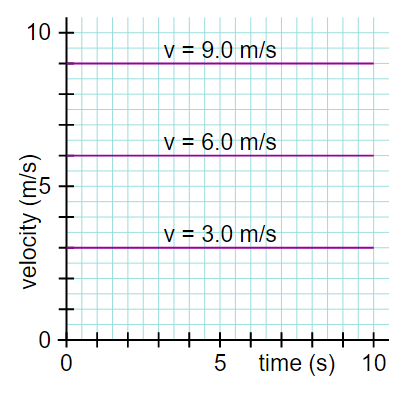
What does the slope on a velocity-time graph mean?
When the line on a velocity-time graph is straight but not horizontal, the velocity is changing.
The three lines to the right each have a different slope. The graph with the steepest slope experiences the fastest change in velocity. That object has the greatest acceleration.
The slope of a velocity time graph represents the acceleration.
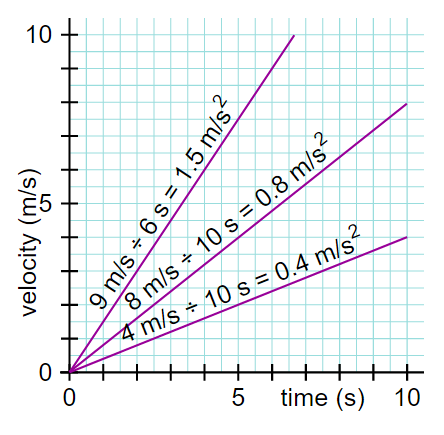
What is the equation of the line?
The relationship between velocity and time is given by one of the suvat equations:
Thus, in the case of constant acceleration, a graph of v over t should be a straight line with gradient a. The initial velocity, u is the y-intercept.
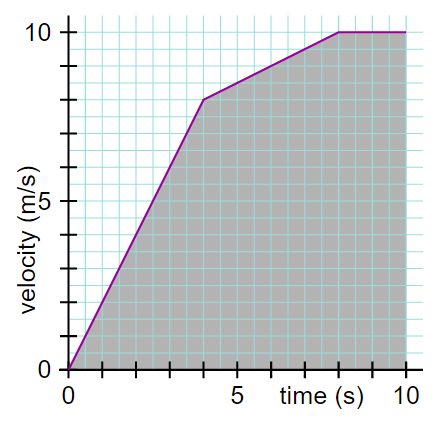
What is the area under the line?
In a velocity – time graph, the area under the line is significant.
How to calculate area?
In a v – t graph, the area under the line represents the quantity velocity x time.

Even in cases of changing velocity, the area between the line and the time-axis represents the displacement of the object.
Acceleration-time graphs
Acceleration – time graphs
These graphs show the acceleration of an object over a period of time.
For straight line motion, a negative acceleration would be when the object is experiencing a change in velocity in the opposite direction to that which was defined as positive.
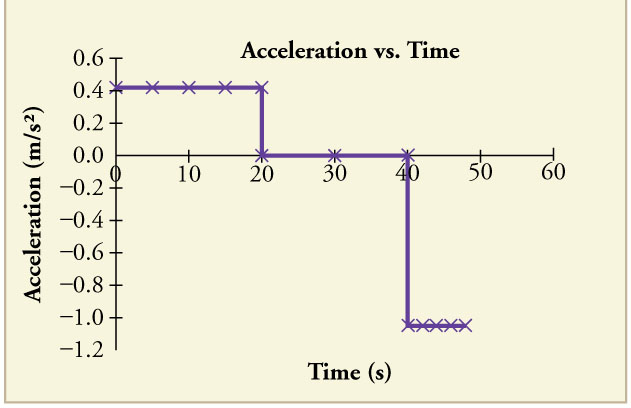
What is the area under acceleration – time graphs?
By finding the area under an acceleration vs time graph, we are multiplying acceleration by time.
What quantity is equal to acceleration time time?
The area under the line of an acceleration-time graph is equal to the change in velocity, Δv. Note that this is the change, not the actual velocity.
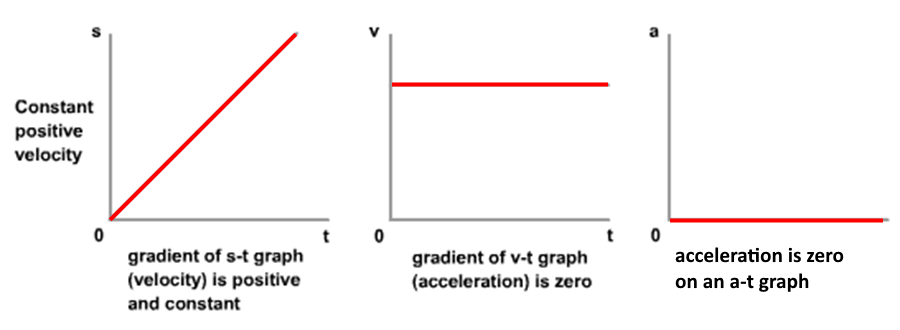
Graphs of constant acceleration (zero)
Graphs of constant acceleration (positive)
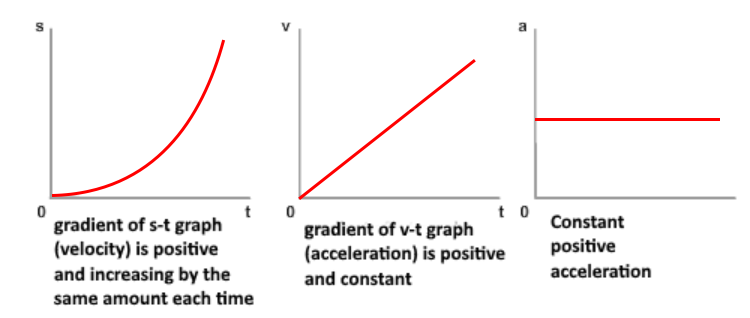
Graphs of constant acceleration (negative)
