5.2 Motion on a Plane

Vectors

Why do we need vectors?

So far, all our problems have been in ONE dimension (e.g. left/right, east/west). In these situations, it isn’t easy to see why vectors are important.  

Quite often, motion is in two or three dimensions. In year 11, we focus on problems in two dimensions, or motion on a plane. 

Examples of motion in two dimensions include: a car which travels east then north, or projectiles moving through the air.

To calculate the speed or velocity of the object shown at the moment it hits the ground we need to consider both its horizontal velocity vector and its vertical velocity vector. 

How to draw vectors?

Vectors are represented with an arrow: its length represents magnitude and its direction represents the vector’s direction.

By using arrows to represent vectors, we can represent vector problems visually, which helps us to solve them.

Only size and direction matters, so a vector arrow can be moved to anywhere on the page as long as length and direction don’t change.

How to add vectors using vector diagrams?

When vector quantities are added, the labelled arrows that represent the vectors are placed ‘head to tail’. 

The “sum of the vectors” is represented by the arrow drawn from the tail of the first vector to the head of the second vector. 

The vector sum is also called the resultant vector. 

You cannot find the magnitude of the resultant vector without considering the direction of the vectors. 

How to find the resultant vector?

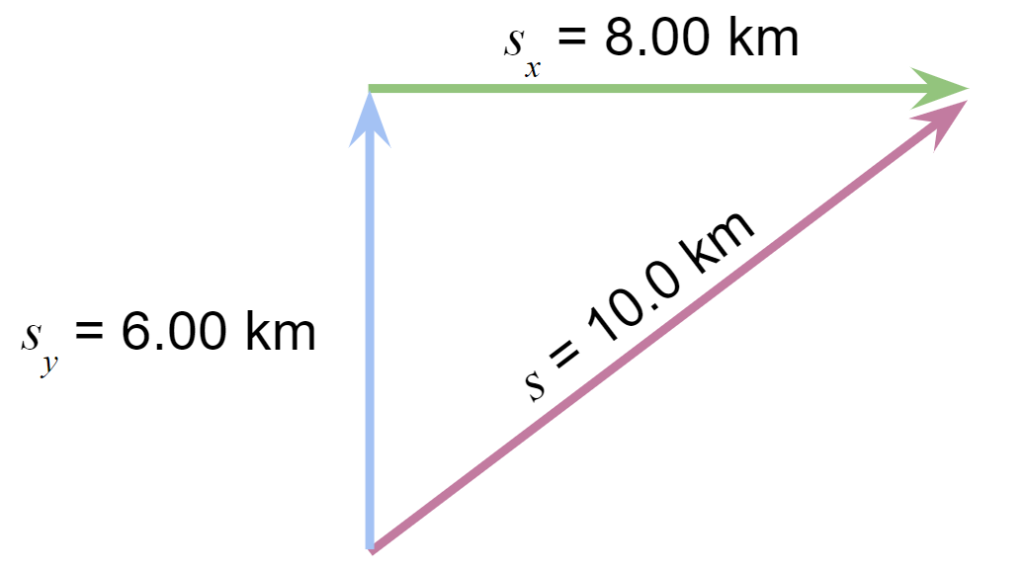
A cyclist travelled 8.00 km east before travelling 6.00 km north. What is the magnitude of their displacement?  

In this example, the resultant vector,  

We must use Pythagoras to work out the magnitude of the vector: 

Simply adding the magnitude of the vectors gives a completely wrong answer: 

s = s_x + s_y = 14 km

Does the order of the vectors matter? 

The order in which the vectors are added doesn’t matter. 

If the cyclist travelled 8.00 km east before travelling 6.00 km north the resultant vector or “sum” of the displacement vectors would be the same; that is, s = 10.0 km. 

How to show direction? 

When describing the direction of a vector on a horizontal plane, there are two options: Compass bearings or directions relative to North/South.

Bearings are the angle of the direction clockwise from North (E.g. Bearing 250°)

The Relative Direction is direction relative to North or South. (E.g. S 32° W – meaning from South, go 32 degrees toward the West). 

Note that the convention is to say North-East and North-West rather than East-North or West-North.

Projectile motion

What forces act on a projectile? 

There are only two forces acting on a projectile: gravity and air resistance. In this course we will usually ignore air resistance.

What is the misconception? 

Many people believe that for an object to be in motion there must be a force acting on it in the direction of that motion. 

This is not true.  

Recall Newton’s First Law of motion. No force is required to make the football continue moving once it has started moving (although air resistance will act on the ball).

What is a projectile? 

We can define a projectile as an object upon which the only force acting is gravity.

Examples of projectiles include (provided that the influence of air resistance is negligible):

• an object dropped from rest 
• an object which is thrown vertically upwards 
• and an object is which thrown upwards at an angle 

The independence of horizontal and vertical motion

How does the motion of projected and dropped objects compare?

In the video, two balls are released from the same height at the same time. One is dropped and the other is projected (pushed) horizontally.

What did Galileo notice? 

The motion of a projectile can be regarded as two separate and independent motions superimposed upon each other. 

The first is a vertical motion, which is subject to acceleration due to gravity

The second is a horizontal motion, which experiences no acceleration. 

What are the components of a projectile’s acceleration? 

The acceleration of a projectile is:

Horizontally, a_x = 0 ms^-2 because there is no horizontal force

Vertically, a_y = g = 9.81 ms^-2 because of the force of gravity.

So the acceleration of a projectile is always directly downwards. 

(Remember, objects only accelerate if there is a net force, and they accelerate in the direction of the net force)

What is a trajectory? 

The path taken by a projectile is called a trajectory. 

In the absence of air resistance, the trajectory is parabolic.

How does the acceleration of a projectile change? 

The image is a graph of the vertical and horizontal components of displacement. The projectile’s position is plotted at equal time intervals. 

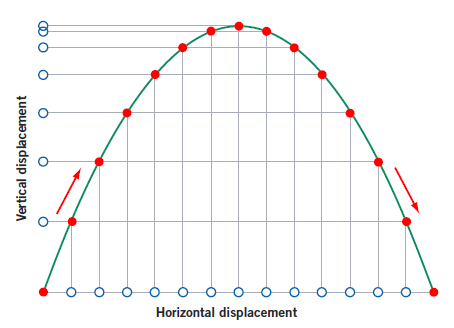
How can you tell that this projectile experiences no acceleration in the horizontal direction?  

How does the velocity of a projectile change? 

The acceleration of a projectile is directly downwards:

a_y = g = -9.81 ms^-2

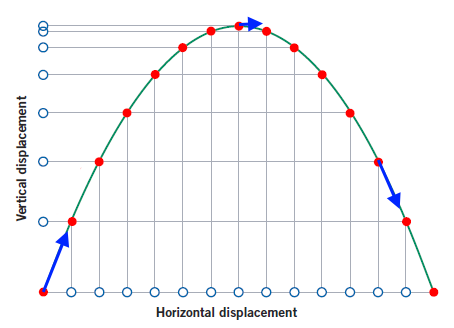
This does not mean that the velocity is directly downwards. Remember that acceleration is the change in velocity over time; velocity and acceleration do not need to be in the same direction. The force on any projectile is always downwards, but the direction of motion can be in any direction, including upwards.

Projectiles launched horizontally

The initial vertical velocity of a projectile launched horizontally is zero.

Adapting the acceleration equations for vertical motion

In adapting the acceleration equations for vertical motion we use the following variables:

a_y = -9.8 ms^-2. I almost always use a negative value because I’ll represent directions upwards with a positive value. 

v_y
u_y
s_y 

So you’ll see me write equations like this: v_y = u_y + a_yt

Adapting the acceleration equations for vertical motion

In adapting the acceleration equations for horizontal motion we need to note the following variables:

a_x = 0 ms^-2
v_x
u_x
s_x

Because a_x = 0 ms^-2 our equations for the horizontal motion become very simple.

How to calculate the final velocity of a projectile?

1. Remember that the horizontal component of the velocity doesn’t change: u_x = v_x.  
2. Determine the final velocity of the vertical component using v = u + at 
3. “Add” the vector components to find the resultant vector. Remember, adding the vector components involves using:  

How to calculate the flight time?

1. Remember the vertical component of the initial velocity, u_y = 
2. Calculate the flight time, t, using

How to calculate the range? 

1. We need the horizontal component of the initial velocity, u_x
2. Analyse the vertical motion to find the total journey time. 
3. Calculate the range, s_x, using: 

Motion graphs for horizontally launched projectiles

The motion graphs for horizontally launched projectiles are graphs of constant acceleration.

Remember, horizontally, the acceleration is zero. Vertically, the magnitude of the acceleration is 9.81 m s^-2. Don’t forget to show the direction of the acceleration on the graph.