5.4 Momentum

What does momentum depend on? 

The momentum of an object, p, is the mass of the object multiplied by its velocity.

\[ \vec p = m \vec v \]
  • what are the base SI units of momentum?
    • Since 1 N = 1 kg ms-2, the units for momentum can be expressed as N s
    • The momentum of a moving object is a measure of the average force required to stop the object in 1 s !

Momentum is a vector quantity. What is the direction of the momentum of an object?

Why use the concept of momentum? 

The law of conservation of momentum allows us to solve many problems, especially problems involving interactions between different objects, and explosions. 

Also, Newton’s second law (Fnet = ma) is only valid when the mass of the system remains constant. But there are many situations where the mass does not remain constant. For example:

  • the motion of a rocket, where the mass decreases due to burnt fuel ejected away from the rocket
  • sand falling on a conveyor belt so the mass increases

Note that we won’t deal with problems involving change in mass in this course. 

What did Newton have to say about momentum? 

Newton actually wrote his second law in terms of momentum rather than acceleration.

Newton’s Second Law of Motion, when translated from the original Latin reads:

The rate of change of momentum is directly proportional to the magnitude of the net force and is in the direction of the net force.

\[ \vec F_{net}=\frac{\Delta \vec p}{\Delta t} \]

Note that this notation for vector quantities isn’t used in TASC Physical Sciences.

What is Newton’s Second Law in terms of Momentum? 

What is an impulsive force? 

A large force exerted during a short interval of time is called an impulsive force. The forces of a hammer on a nail and of a bat on a baseball are other examples of impulsive forces.

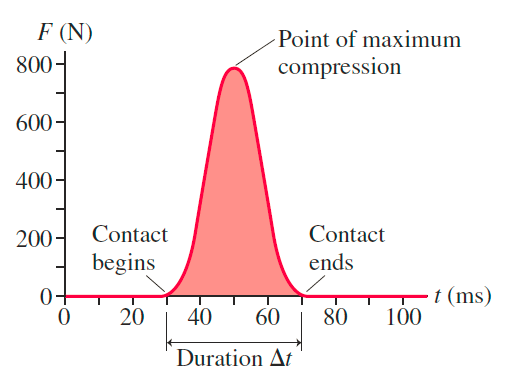
The force acting on a soccer ball over time.

What is the impulse? 

The relationship between the net force applied to an object and its momentum can be explored by applying Newton’s Second Law of Motion to the object.

The product FnetΔt is called the impulse of the net force. 

The impulse of any force is defined as the product of the force and the time interval over which it acts. 

The impulse is equal to the change in momentum. 

How does impulse explain impact forces? 

From Δp = FnetΔt , a change in momentum can be achieved with a small force acting for a long time or large force acting for a short time.

For example, when you drop from a height of, say, 1 m, you will land on the ground with a speed of about 4.5 m s−1. If your mass is 60 kg, your momentum just before landing (your initial momentum) will be 270 kg m s-1 and will become zero after you land (final momentum = o). Your change in momentum, Δp = – 270 kg m s-1 downwards.

Experience should tell you that you will experience a large force if you do not bend your knees upon landing − keeping your knees stiff means that you will come to rest in a short time. This means Δt will be very small. As a result, the force acting on you will be large (which may damage your knees).

How to explain impact forces? 

To understand the effect of changing the initial velocity and impact time on the force required to change the momentum, consider the momentum equation:  

\[ F_{net}=\frac{\Delta p}{\Delta t}=\frac{m(v-u)}{t} \]

As initial velocity, u, increases, the magnitude of the force required to stop a body increases.

As the stopping time, t, increases, the force required to stop a body decreases.