On Thursday, April 11, 2019, a SpaceX Falcon Heavy rocket launched the Arabsat-6A satellite from Launch Complex 39A at NASA’s Kennedy Space Center in Florida. Credits: SpaceX

What is the law of conservation of momentum? 

Momentum is a conserved quantity. For a conserved quantity, the total amount of that quantity in the universe, or in any isolated system, remains constant.

The sum of the momentum of all the objects in an isolated system remains constant:

\[ \sum \vec p_{initial} = \sum \vec p_{final} \]

Why is it important to consider the direction of momentum?

The total initial momentum of the can and its contents (before the explosion) is zero.

The total final momentum of the can and its contents (after the explosion) must also equal zero. This is only possible if we consider the direction of momentum.

The top of the can and some of the contents has momentum to the right. The bottom of the can and some of the contents has momentum to the left. Some contents sprays upwards. If we add all these momenta, the total will equal zero.

What is the system?

Is a falling ball an isolated system? 

Consider a ball that you drop from rest from a certain height. As the ball falls, its speed and hence its momentum increases so momentum does not stay the same.

This is because there is an external force on the ball, namely its weight. So the momentum of the system that consists of just the falling ball is not conserved. 

Why doesn’t the Earth move?

If we include the Earth as part of the system then there are no external forces and the total momentum will be conserved.

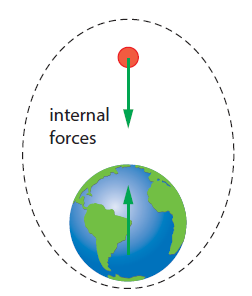
This means that the momentum of the Earth must change as the ball falls! 

So why don’t we notice a change in speed of the Earth? The change in speed of the Earth is negligible because the mass of the Earth is so large.

What is the system for a rocket in flight?

The system for a rocket in flight is not the rocket and the Earth. Rockets can be propelled without the Earth. 

The relevant system is the rocket and exhaust gases. The change in momentum of the exhaust gases is equal and opposite to the change in momentum of the rocket.  

How is momentum related to Newton’s Third Law?

Extension:

In any interaction between two objects, both experience a force, and these forces are equal in magnitude and opposite in direction. 

\[ F_{A\,on\,B} = -F_{B\,on\,A} \]

We can write Newton’s second law in terms of rate of change of momentum and substitute this in to Newton’s third law: 

\[ F_{A\,on\,B} =\frac{\Delta p_B}{\Delta t}=-\frac{\Delta p_A}{\Delta t} -F_{B\,on\,A} \]
\[ \frac{\Delta p_B}{\Delta t}=-\frac{\Delta p_A}{\Delta t} \]

Because the time during which the interaction takes place must be the same for both objects,

\[ \Delta p_B=-\Delta p_A \]

This tells us that in any interaction between two objects, A and B, the change in momentum of A is equal but opposite to the change in momentum of B.

We can also write this as:

\[ \Delta p_B + \Delta p_A = 0 \]

which is simply saying that in any interaction between two objects, the total change in momentum is zero. Hence, Newton’s third law is really a statement of conservation of momentum.